10 Elementary Integrals
10.1 The Existence-Construction Gap
The Fundamental Theorem establishes that continuous functions possess antiderivatives. Theorem 9.1 guarantees existence: given f continuous on [a,b], the function F(x) = \int_a^x f(t)\,dt satisfies F' = f. Yet this is an existence proof—it provides an antiderivative implicitly, as an accumulation function, without offering an explicit formula.
For evaluation purposes, Theorem 9.4 requires an antiderivative in closed form. Given F with F' = f, we compute \int_a^b f = F(b) - F(a). But how do we find F?
For many functions—polynomials, exponentials, trigonometric functions—we know antiderivatives by inspection, reversing differentiation rules. For f(x) = x^n, we have F(x) = x^{n+1}/(n+1). For f(x) = e^x, we have F(x) = e^x. For f(x) = \sin x, we have F(x) = -\cos x.
But this is ad hoc. Can we systematize antiderivative computation? Can we derive all elementary antiderivatives from a unified principle? (For quick verification, try our integral calculator.)
The answer lies in analyticity and term-by-term integration.
10.2 Analytic Functions and Series Representations
Recall from Section 7.5 that a function f is analytic at a if it equals its Taylor series in some neighborhood of a: f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n for all x in an interval (a-R, a+R) with R > 0. The function is completely determined by its derivatives at a—all information about f is encoded in the sequence \{f^{(n)}(a)\}.
Most functions encountered in elementary calculus are analytic:
Polynomials (everywhere)
e^x (everywhere)
\sin x, \cos x (everywhere)
\ln(1+x) (for |x| < 1)
(1+x)^\alpha (for |x| < 1, any \alpha)
Rational functions (away from poles)
These functions possess convergent power series representations. This structure is useful, as it turns out, if f is analytic we can integrate it term-by-term.
10.3 Term-by-Term Integration
Theorem 10.1 (Term-by-Term Integration) Let f(x) = \sum_{n=0}^{\infty} c_n (x-a)^n converge absolutely for |x-a| < R. Then f is integrable on any closed subinterval of (a-R, a+R), and \int_a^x f(t)\,dt = \sum_{n=0}^{\infty} c_n \int_a^x (t-a)^n\,dt = \sum_{n=0}^{\infty} c_n \frac{(x-a)^{n+1}}{n+1} for |x-a| < R.
Fix x with |x-a| < R and choose r with |x-a| < r < R. The interval from a to x is contained in the disk of radius r. Since \sum |c_n| r^n < +\infty and |c_n(t-a)^n| \leq |c_n|r^n for all t between a and x, the Weierstrass M-test shows that \sum c_n(t-a)^n converges uniformly on this interval. Uniform convergence of continuous functions permits interchange of limit and integral, so \int_a^x f(t)\,dt = \int_a^x \lim_{N\to\infty} \sum_{n=0}^N c_n(t-a)^n\,dt = \lim_{N\to\infty} \sum_{n=0}^N c_n \int_a^x (t-a)^n\,dt = \sum_{n=0}^{\infty} c_n \frac{(x-a)^{n+1}}{n+1}.\qquad\square
The proof requires uniform convergence—a condition ensuring that limits and integrals commute.
The intuition is straightforward: if f is a sum of functions, and each term can be integrated, we integrate term-by-term. The series \sum_{n=0}^{\infty} c_n (x-a)^n becomes \sum_{n=0}^{\infty} c_n \frac{(x-a)^{n+1}}{n+1}.
Each monomial (x-a)^n integrates to (x-a)^{n+1}/(n+1), and the series structure is preserved. The antiderivative is itself a power series, converging on the same interval.
To find \int f(x)\,dx for an analytic function, expand f as a power series, integrate term-by-term, and add the constant of integration.
Note on uniform convergence. The technical justification for term-by-term integration invokes uniform convergence: if f_n \to f uniformly on [a,b] and each f_n is continuous, then \int_a^b f = \lim_{n \to \infty} \int_a^b f_n.
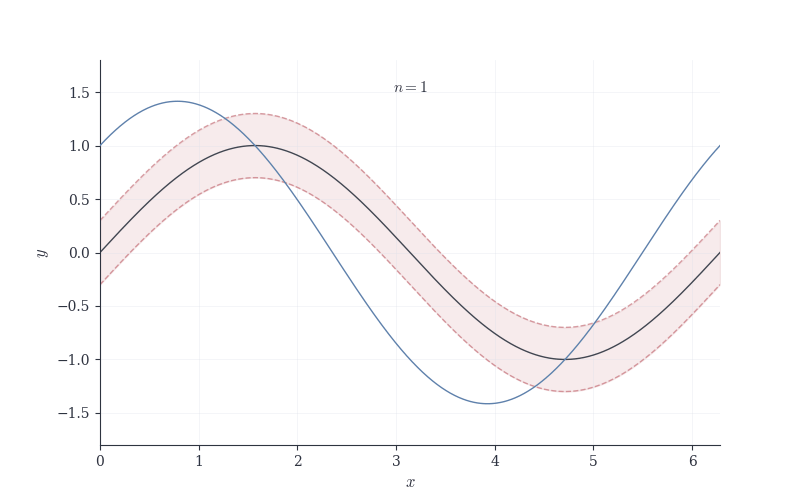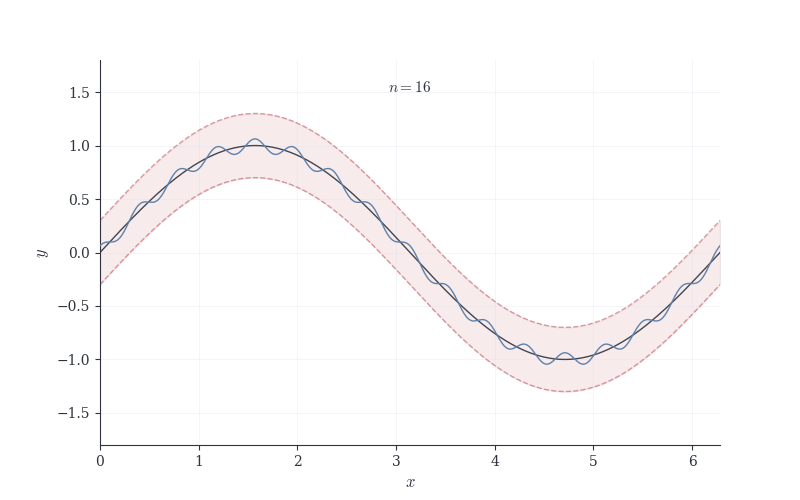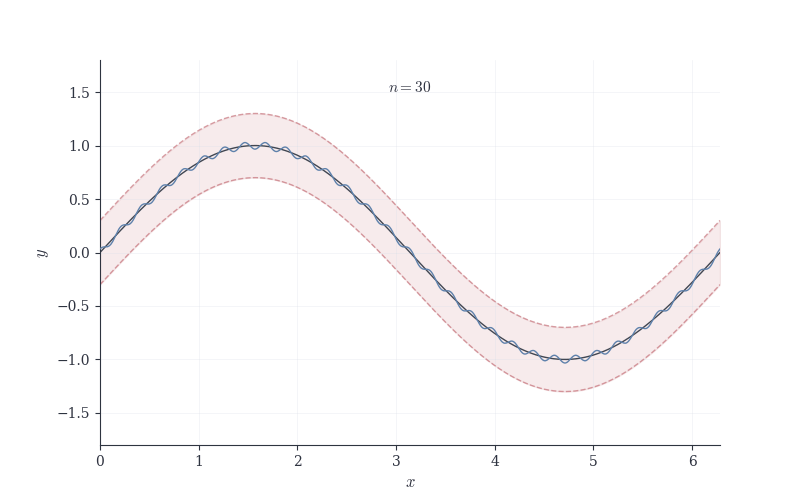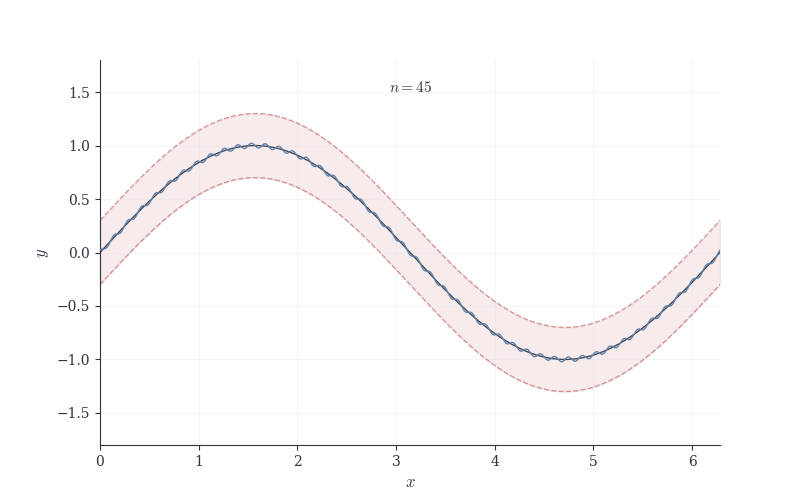
The animation shows f_n converging uniformly to f. The \varepsilon-tube (shaded red region) surrounds the limit function. As n increases, the blue curve settles entirely within this tube—uniform convergence means the entire graph fits for all x simultaneously once n is large enough.
For power series within their radius of convergence, uniform convergence holds automatically. We defer the precise statement to § Uniform Continuity (optional) or a course on real analysis, but the upshot is clear: for functions we encounter in this course—polynomials, exponentials, trigonometric functions, and their compositions—term-by-term integration is valid.
Functions admitting Taylor series representations are “sufficiently smooth” that integration and summation commute. We need not verify uniform convergence each time; analyticity guarantees it.
10.4 Deriving Elementary Antiderivatives
We now derive antiderivatives of elementary functions using their power series.
10.4.1 Polynomials
A polynomial f(x) = \sum_{k=0}^n a_k x^k is already a finite power series. Integrate term-by-term: \int f(x)\,dx = \sum_{k=0}^n a_k \int x^k\,dx = \sum_{k=0}^n a_k \frac{x^{k+1}}{k+1} + C.
Each monomial x^k integrates to x^{k+1}/(k+1), the reverse of the power rule (x^{k+1})' = (k+1)x^k.
10.4.2 The Exponential Function
From Section 7.5, we know e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} with radius of convergence R = \infty. Integrate term-by-term: \int e^x\,dx = \int \sum_{n=0}^{\infty} \frac{x^n}{n!}\,dx = \sum_{n=0}^{\infty} \frac{1}{n!} \int x^n\,dx = \sum_{n=0}^{\infty} \frac{x^{n+1}}{(n+1) \cdot n!} + C.
Simplify, (n+1) \cdot n! = (n+1)!, so \int e^x\,dx = \sum_{n=0}^{\infty} \frac{x^{n+1}}{(n+1)!} + C = \sum_{m=1}^{\infty} \frac{x^m}{m!} + C, where m = n+1. But \sum_{m=1}^{\infty} \frac{x^m}{m!} = e^x - 1, hence \int e^x\,dx = e^x - 1 + C.
Redefining the constant as C' = C - 1, we obtain \int e^x\,dx = e^x + C'.
The exponential function is its own antiderivative. This is immediate from the series: shifting the index increases each term’s power by one while multiplying by the same factor that appears in the factorial denominator.
10.4.3 Sine and Cosine
From Section 7.5: \sin x = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!}, \quad \cos x = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n}}{(2n)!}.
Integrate sine term-by-term \int \sin x\,dx = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} \int x^{2n+1}\,dx = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+2}}{(2n+2) \cdot (2n+1)!} + C.
Simplify (2n+2) \cdot (2n+1)! = (2n+2)!, so \int \sin x\,dx = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+2}}{(2n+2)!} + C = \sum_{m=1}^{\infty} \frac{(-1)^{m-1} x^{2m}}{(2m)!} + C, where m = n+1. The series \sum_{m=1}^{\infty} \frac{(-1)^{m-1} x^{2m}}{(2m)!} equals -\sum_{m=1}^{\infty} \frac{(-1)^m x^{2m}}{(2m)!}. Adding the missing zeroth term: \sum_{m=0}^{\infty} \frac{(-1)^m x^{2m}}{(2m)!} = \cos x.
Thus \sum_{m=1}^{\infty} \frac{(-1)^m x^{2m}}{(2m)!} = \cos x - 1, whence \int \sin x\,dx = -(\cos x - 1) + C = -\cos x + C', redefining C' = C + 1.
Similarly, integrate cosine \int \cos x\,dx = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n)!} \int x^{2n}\,dx = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!} + C = \sin x + C.
These derivations confirm the antiderivatives. The structure is transparent: shifting indices in the series corresponds to integrating term-by-term.
10.4.4 The Natural Logarithm
The logarithm arises as the antiderivative of 1/x, but we derive it via series. Consider \ln(1+x) = \int_0^x \frac{1}{1+t}\,dt.
From the geometric series (Section 7.5): \frac{1}{1+t} = \sum_{n=0}^{\infty} (-1)^n t^n for |t| < 1. Integrate term-by-term: \ln(1+x) = \int_0^x \sum_{n=0}^{\infty} (-1)^n t^n\,dt = \sum_{n=0}^{\infty} (-1)^n \int_0^x t^n\,dt = \sum_{n=0}^{\infty} \frac{(-1)^n x^{n+1}}{n+1}.
This is the Mercator series (1668): \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots
converging for |x| < 1 (and also at x = 1 by the alternating series test).
Differentiating term-by-term recovers \frac{1}{1+x}, confirming that \ln(1+x) is the antiderivative of \frac{1}{1+x}.
For the general logarithm, use substitution. Let u = 1 + x, so x = u - 1 and dx = du. Then \int \frac{1}{u}\,du = \ln|u| + C.
More precisely, \ln|x| is the antiderivative of 1/x for x \neq 0. The absolute value accounts for negative arguments.
10.4.5 Power Functions
For f(x) = x^\alpha with \alpha\in\mathbb{R} \setminus\{-1\}, we have \int x^\alpha\,dx = \frac{x^{\alpha+1}}{\alpha+1} + C.
Again, this follows from the power rule (x^{\alpha+1})' = (\alpha+1)x^\alpha applied in reverse. The case \alpha = -1 yields the logarithm as shown above.
For fractional or negative exponents, the result remains valid provided x > 0 (or appropriate domain restrictions). For instance, \int x^{1/2}\,dx = \frac{2x^{3/2}}{3} + C, \quad \int x^{-2}\,dx = -x^{-1} + C.
10.5 Summary: The Standard Antiderivatives
We have derived the following antiderivatives from first principles using power series:
| Function f(x) | Antiderivative F(x) + C | Domain |
|---|---|---|
| x^n (n \neq -1) | \frac{x^{n+1}}{n+1} + C | \mathbb{R} (or \mathbb{R}^+ if n < 0) |
| \frac{1}{x} | \ln\|x\| + C | \mathbb{R} \setminus \{0\} |
| e^x | e^x + C | \mathbb{R} |
| \sin x | -\cos x + C | \mathbb{R} |
| \cos x | \sin x + C | \mathbb{R} |
These are the elementary antiderivatives—the building blocks for integration. All other antiderivatives are obtained via:
Linearity: \int [af(x) + bg(x)]\,dx = a\int f(x)\,dx + b\int g(x)\,dx
Substitution (change of variables, covered in the next chapter)
Integration by parts (covered subsequently)
Partial fractions (for rational functions)
Remark. Certain elementary antiderivatives evaluate to inverse‑trigonometric functions; the study of these cases is postponed until the treatment of trigonometric substitution, which both motivates and explains the occurrence of such antiderivatives.
10.6 Remarks on Analyticity
As mentioned, the functions we integrate in this course—polynomials, exponentials, trigonometric functions, logarithms, and combinations thereof—are analytic on appropriate domains. This has two consequences:
Term-by-term operations are valid. We can differentiate and integrate power series term-by-term without verifying technical conditions each time. Analyticity guarantees that limits and operations commute.
Antiderivatives exist and are computable. Every analytic function has an antiderivative that is itself analytic. The antiderivative may not always be expressible in terms of elementary functions (e.g., \int e^{-x^2}\,dx has no closed form), but it exists as a power series.
The machinery we developed in Section 7.5 now pays dividends: Taylor series are not just approximations—they provide exact representations. When we write e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!},
this is not an approximation. It is the function e^x, expressed as an infinite polynomial. Integrating this series term-by-term yields the antiderivative exactly.
Contrast with non-analytic functions. The function f(x) = \begin{cases} e^{-1/x^2} & x \neq 0 \\ 0 & x = 0 \end{cases} is smooth but not analytic at x = 0 (see Section 7.8). Its Taylor series at 0 is identically zero, failing to represent f. Such pathologies do not arise for the functions we encounter in elementary calculus.
This is why we emphasize analyticity. It is not pedantry—it is the structural property that makes calculus tractable. Functions admitting power series representations are “well-behaved” in a precise sense: they can be manipulated algebraically, integrated term-by-term, and differentiated freely. The interplay between local information (derivatives at a point) and global behavior (the function everywhere) is “seamless.”
10.7 Beyond Elementary Antiderivatives
We revisit the function f(x) = e^{-x^2} (the Gaussian) which as we know has no antiderivative expressible in terms of polynomials, exponentials, logarithms, and trigonometric functions. Yet it has an antiderivative as a power series \int e^{-x^2}\,dx = \int \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n}}{n!}\,dx = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)n!} + C.
This series defines the error function \text{erf}(x), central to probability theory and statistics. It is a perfectly well-defined function—differentiable, integrable, analytic—despite lacking a closed form.
The takeaway is that antiderivatives always exist for continuous functions (by Theorem 9.1), but they may not be elementary. Power series provide a way to compute and represent such antiderivatives, extending our toolkit beyond the standard table of integrals.
Subsequent chapters develop techniques—substitution, integration by parts, partial fractions—that expand the class of functions for which we can find closed-form antiderivatives. But the foundational insight remains: integration is the inverse of differentiation, and analytic functions admit term-by-term integration. This is the principle underlying all antiderivative computations.
Term-by-term integration and the construction of antiderivatives.
Use the geometric series \frac{1}{1-x} = \sum_{n=0}^{\infty} x^n for |x| < 1 to derive a power series representation for \ln(1-x) by integrating term-by-term from 0 to x. Verify your answer by differentiating the resulting series.
Show that \ln 2 = \sum_{n=1}^{\infty} \frac{1}{n \cdot 2^n} by evaluating your series from part (a) at x = 1/2. Prove that this series converges using the comparison test.
Consider the function f(x) = \frac{1}{1+x^2}. Expand f as a power series by substituting -x^2 into the geometric series. Integrate term-by-term from 0 to x to obtain a series representation for \arctan x. Evaluate this series at x = 1 to discover a remarkable formula for \pi.
Antiderivatives of analytic functions and uniform convergence.
Let f(x) = \sum_{n=1}^{\infty} \frac{x^n}{n} for |x| < 1. Show that f is continuous on (-1,1) and that f'(x) = \frac{1}{1-x} by differentiating the series term-by-term. Deduce that f(x) = -\ln(1-x) for |x| < 1.
Using the result from part (a), prove that the series \sum_{n=1}^{\infty} \frac{x^n}{n} converges uniformly on [-r, r] for any 0 < r < 1. Then explain why we can integrate this series term-by-term over any interval [a,b] \subset (-1,1).
The series \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n} converges by the alternating series test. Use Abel’s theorem (which states that if \sum a_n x^n converges at x = R, then \lim_{x \to R^-} \sum a_n x^n = \sum a_n R^n) together with your result from part (a) to prove that \ln 2 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots
Computing definite integrals via series expansions.
Consider I = \int_0^{1/2} \frac{\sin x}{x} \, dx. Although \frac{\sin x}{x} has no elementary antiderivative, expand \sin x as a Taylor series and divide by x to obtain a series representation for \frac{\sin x}{x}. Integrate this series term-by-term from 0 to 1/2 to compute I as an infinite series.
Prove that the series you obtained in part (a) converges absolutely. Then determine how many terms are required to approximate I to within 10^{-4}. (Hint: Use the alternating series estimation theorem.)
Generalize the method from part (a) to express \int_0^x \frac{\sin t}{t} \, dt as a power series in x. Verify that your series is well-defined at x = 0 by showing that \lim_{x \to 0} \frac{\sin x}{x} = 1. This function is called the sine integral, denoted \text{Si}(x), and appears frequently in applications despite having no elementary form.
Term-by-term integration and the construction of antiderivatives.
Deriving the series for \ln(1-x). From the geometric series, \frac{1}{1-x} = \sum_{n=0}^{\infty} x^n for |x| < 1. Integrating both sides from 0 to x, \int_0^x \frac{1}{1-t} \, dt = \int_0^x \sum_{n=0}^{\infty} t^n \, dt.
By Theorem 10.1, we integrate term-by-term, -\ln(1-x) = \sum_{n=0}^{\infty} \int_0^x t^n \, dt = \sum_{n=0}^{\infty} \frac{x^{n+1}}{n+1}.
Reindexing with m = n+1, -\ln(1-x) = \sum_{m=1}^{\infty} \frac{x^m}{m}.
Thus, \ln(1-x) = -\sum_{n=1}^{\infty} \frac{x^n}{n}.
To verify, differentiate term-by-term. Since power series can be differentiated within their radius of convergence, \frac{d}{dx}\left[-\sum_{n=1}^{\infty} \frac{x^n}{n}\right] = -\sum_{n=1}^{\infty} x^{n-1} = -\sum_{k=0}^{\infty} x^k = -\frac{1}{1-x}.
But \frac{d}{dx}[\ln(1-x)] = \frac{-1}{1-x}, confirming our result. \square
Evaluating at x = 1/2. From part (a), \ln(1-x) = -\sum_{n=1}^{\infty} \frac{x^n}{n}.
Setting x = 1/2, \ln(1/2) = -\ln 2 = -\sum_{n=1}^{\infty} \frac{1}{n \cdot 2^n}.
Therefore, \ln 2 = \sum_{n=1}^{\infty} \frac{1}{n \cdot 2^n}.
To prove convergence, note that for n \geq 1, \frac{1}{n \cdot 2^n} \leq \frac{1}{2^n}.
Since \sum_{n=1}^{\infty} \frac{1}{2^n} is a convergent geometric series (with sum 1), the comparison test yields convergence of \sum_{n=1}^{\infty} \frac{1}{n \cdot 2^n}. \square
Series for \arctan x and a formula for \pi. Starting with the geometric series, \frac{1}{1+u} = \sum_{n=0}^{\infty} (-1)^n u^n for |u| < 1. Substitute u = x^2, \frac{1}{1+x^2} = \sum_{n=0}^{\infty} (-1)^n x^{2n}.
Integrate from 0 to x, \int_0^x \frac{1}{1+t^2} \, dt = \int_0^x \sum_{n=0}^{\infty} (-1)^n t^{2n} \, dt.
By Theorem 10.1, \arctan x = \sum_{n=0}^{\infty} (-1)^n \int_0^x t^{2n} \, dt = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{2n+1}.
Setting x = 1, \arctan 1 = \sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots
Since \arctan 1 = \pi/4, we obtain the Leibniz formula, \frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots
This remarkable identity expresses \pi as an alternating sum of reciprocals of odd integers. \square
Antiderivatives of analytic functions and uniform convergence.
Identifying f as -\ln(1-x). The series f(x) = \sum_{n=1}^{\infty} \frac{x^n}{n} converges absolutely for |x| < 1 by the ratio test, \lim_{n \to \infty} \frac{|x|^{n+1}/(n+1)}{|x|^n/n} = \lim_{n \to \infty} \frac{n|x|}{n+1} = |x| < 1.
Power series are continuous within their radius of convergence, so f is continuous on (-1,1).
Differentiating term-by-term (valid within the radius of convergence), f'(x) = \sum_{n=1}^{\infty} \frac{d}{dx}\left(\frac{x^n}{n}\right) = \sum_{n=1}^{\infty} x^{n-1} = \sum_{k=0}^{\infty} x^k = \frac{1}{1-x}.
Since f'(x) = \frac{1}{1-x} and \frac{d}{dx}[-\ln(1-x)] = \frac{1}{1-x}, we have f(x) = -\ln(1-x) + C for some constant. Evaluating at x = 0, f(0) = 0 = -\ln 1 + C = C.
Thus f(x) = -\ln(1-x) for |x| < 1. \square
Uniform convergence on compact subintervals. Fix 0 < r < 1. For |x| \leq r, \left|\frac{x^n}{n}\right| \leq \frac{r^n}{n}.
The series \sum_{n=1}^{\infty} \frac{r^n}{n} converges (as shown in part (a), it equals -\ln(1-r)). By the Weierstrass M-test, \sum_{n=1}^{\infty} \frac{x^n}{n} converges uniformly on [-r, r].
Uniform convergence of continuous functions preserves integrability and permits interchange of limit and integral. Therefore, for any [a,b] \subset (-1,1), we can choose r with \max(|a|, |b|) < r < 1. The series converges uniformly on [a,b], so \int_a^b f(x) \, dx = \int_a^b \sum_{n=1}^{\infty} \frac{x^n}{n} \, dx = \sum_{n=1}^{\infty} \int_a^b \frac{x^n}{n} \, dx.
This justifies term-by-term integration over any closed subinterval of (-1,1). \square
Using Abel’s theorem. From part (a), we have -\ln(1-x) = \sum_{n=1}^{\infty} \frac{x^n}{n} for |x| < 1. Substituting x \to -x, -\ln(1+x) = \sum_{n=1}^{\infty} \frac{(-x)^n}{n} = \sum_{n=1}^{\infty} \frac{(-1)^n x^n}{n}.
Thus, \ln(1+x) = \sum_{n=1}^{\infty} \frac{(-1)^{n-1} x^n}{n} = \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n} x^n.
The series \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n} converges by the alternating series test. Abel’s theorem states that if \sum a_n x^n converges at x = R, then \lim_{x \to R^-} \sum_{n=0}^{\infty} a_n x^n = \sum_{n=0}^{\infty} a_n R^n.
Applying this with R = 1, \ln 2 = \ln(1+1) = \lim_{x \to 1^-} \ln(1+x) = \lim_{x \to 1^-} \sum_{n=1}^{\infty} \frac{(-1)^{n-1} x^n}{n} = \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n}.
Therefore, \ln 2 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots \quad \square
Computing definite integrals via series expansions.
Series representation for the integral. The Taylor series for \sin x is \sin x = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!}.
Dividing by x, \frac{\sin x}{x} = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n}}{(2n+1)!}.
Integrate from 0 to 1/2, I = \int_0^{1/2} \frac{\sin x}{x} \, dx = \int_0^{1/2} \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n}}{(2n+1)!} \, dx.
By Theorem 10.1, I = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} \int_0^{1/2} x^{2n} \, dx = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} \cdot \frac{(1/2)^{2n+1}}{2n+1}.
Simplifying, I = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!(2n+1) \cdot 2^{2n+1}}. \quad \square
Convergence and approximation. The series is alternating with terms a_n = \frac{1}{(2n+1)!(2n+1) \cdot 2^{2n+1}}.
Since (2n+1)! grows factorially and 2^{2n+1} grows exponentially, a_n \to 0 rapidly. Moreover, a_{n+1} < a_n for all n \geq 0 (verify by computing the ratio). By the alternating series test, the series converges.
The alternating series estimation theorem states that the error in truncating after N terms is bounded by |a_N|. We need a_N = \frac{1}{(2N+1)!(2N+1) \cdot 2^{2N+1}} < 10^{-4}.
Computing the first few terms:
- a_0 = \frac{1}{1 \cdot 1 \cdot 2} = \frac{1}{2} = 0.5
- a_1 = \frac{1}{6 \cdot 3 \cdot 8} = \frac{1}{144} \approx 0.00694
- a_2 = \frac{1}{120 \cdot 5 \cdot 32} = \frac{1}{19200} \approx 0.000052
Since a_2 < 10^{-4}, we need at least N = 2, i.e., three terms of the series to guarantee accuracy within 10^{-4}. \square
The sine integral function. Integrating the series from 0 to x, \text{Si}(x) = \int_0^x \frac{\sin t}{t} \, dt = \int_0^x \sum_{n=0}^{\infty} \frac{(-1)^n t^{2n}}{(2n+1)!} \, dt = \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!(2n+1)}.
At x = 0, every term vanishes except possibly the limit. To verify the function is well-defined at x = 0, we compute \lim_{x \to 0} \frac{\sin x}{x} = \lim_{x \to 0} \frac{\sum_{n=0}^{\infty} \frac{(-1)^n x^{2n+1}}{(2n+1)!}}{x} = \lim_{x \to 0} \sum_{n=0}^{\infty} \frac{(-1)^n x^{2n}}{(2n+1)!} = \frac{1}{1!} = 1.
Thus \text{Si}(0) = 0 and the function is continuous at the origin. The sine integral has no elementary antiderivative, but its power series representation makes it completely well-defined and computable. It appears in diffraction theory, signal processing, and asymptotic analysis. \square